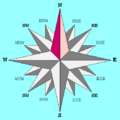
rosa de los vientos

Rosa de los vientos

Copia de la rosa de los vientos de la carta náutica de 1504, del navegante portugués Pedro Reinel. Es la primera rosa de los vientos conocida que representa claramente la flor de lis como símbolo del Norte. Esta práctica fue adoptada en otras cartas náuticas y ha sobrevivido hasta la actualidad.

Una rosa de los vientos es un círculo que tiene marcados alrededor los rumbos en que se divide la circunferencia del horizonte. Su invención se atribuye a Raimundo Lulio, aunque la descripción pormenorizada que da Plinio el viejo en libro II,¹ podría haber sido su referencia básica.
En las cartas de navegación se representa por 32 rombos (deformados) unidos por un extremo mientras el otro señala el rumbo sobre el círculo del horizonte. Sobre el mismo se sitúa la flor de lis con la que suelen representar el Norte que se documenta a partir del siglo XV.
También puede ser un diagrama que representa la intensidad media del vi

Los nombres de los vientos

Nombres tradicionales greco-latinos

Viento	Dirección	Griego	Latino	Franco	Español
N	0° (30° × 0)	Aparctias (ὰπαρκτίας)	Septentrio	Nordroni	Septentrión
NNE	30° (30° × 1)	Meses (μέσης) or Boreas (βoρέας)	Aquilo	Nordostroni	Bóreas
NEE	60° (30° × 2)	Caicias (καικίας)	Caecias	Ostnordroni	Gregal, Cecias
E	90° (30° × 3)	Apeliotes (ὰπηλιώτης)	Subsolanus	Ostroni	Levante
SEE	120° (30° × 4)	Eurus (εΰρος)	Vulturnus	Ostsundroni	Euro
SSE	150° (30° × 5)	Euronotus (εὺρόνοtος)	Euronotus	Sundostroni	Euronoto
S	180° (30° × 6)	Notos (νόtος)	Auster	Sundroni	Noto, Austro
SSW	210° (30° × 7)	Libonotos (λιβόνοtος)	Libonotus or Austroafricus	Sundvuestroni	Libio
SWW	240° (30° × 8)	Lips (λίψ)	Africus	Vuestsundroni	Ábrego
W	270° (30° × 9)	Zephyrus (ζέφυρος)	Favonius	Vuestroni	Céfiro
WNW	300° (30° × 10)	Argestes (ὰργέστης)	Corus	Vuestnordroni	Argestes, Coro
NNW	330° (30° × 11)	Thrascias (θρασκίας)	Thrascias, Circius	Nordvuestroni	Cierzo

Los nombres de los vientos del Mediterráneo

Rosa de los 4 Vientos en el suelo, muy cerca de la Torre de Hércules (La Coruña, Galicia, España), desde donde se ha tomado la foto.

Punto cardinal	Abrev.	Dirección	Viento tradicional (nombre/s)	Abr.v
Norte	N	0°	Tramontana, Terral, Etesio	T
Noreste	NE	45° (45° × 1)	Gregario, Gregal, Greco, Bora	G
Este	E	90° (45° × 2)	Levante	L
Sureste	SE	135° (45° × 3)	Siroco, Chamsin, Marin, Fumeque, Calima	S
Sur	S	180° (45° × 4)	Ostro, Mediodía, Lodos	O
Suroeste	SW	225° (45° × 5)	Lebeche, Libeccio, Garbino	L
Oeste	W	270° (45° × 6)	Poniente, Vendaval	P
Noroeste	NW	315° (45° × 7)	Maestro, Mistral, Galerna, Cierzo	M

Los puntos cardinales

Los cuatro puntos cardinales son:

N - Norte
S - Sur
E - Este
O/W - Oeste

Para identificar mejor estos puntos, se puede usar nuestro cuerpo como referencia. Orientando nuestro frente hacia el Norte, estaría hacia atrás el Sur, a la derecha estaría el Este y la izquierda el Oeste.

Los cuatro rumbos laterales

NE (Norte-Este)-Nordeste
SE (Sur-Este)-Sudeste
SO/SW (Sur-Oeste)-Sudoeste
NO/NW (Norte-Oeste)-Noroeste

Los ocho rumbos colaterales

NNE (Nornordeste)
ENE (Estenordeste)
ESE (Estesudeste)
SSE (Sudsudeste)
SSO/SSW (Sudsudoeste)
OSO/WSW (Oestesudoeste)
ONO/WNW (Oesnoroeste)
NNO/NNW (Nornoroeste)

Los dieciséis rumbos co-colaterales

Los rumbos co-colaterales toman su nombre de los rumbos laterales, agregándoseles "por" (abreviatura p) y en inglés "by" (abreviatura b) para indicar su relación con el rumbo lateral del cual toman su nombre. En la lista a continuación, se colocan los rumbos colaterales en donde no sea claro entre cuales rumbos van.

NpE/NbE (Norte+Norte+Este+Norte)— Norte por el Este

(Nornoreste)

NEpN/NEbN (Norte-Norte-Este-Este)—Nordeste por el Norte
NEpE/NEbE (Este-Norte-Este+Norte)— Nordeste por el Este

(Estenoreste)

EpN/EbN (Este-Norte-Este-Este)— Este por el Norte
EpS/EbS (Este-Sur-Este-Este)— Este por el Sur

(Estesureste)

SEpE/SEbE (Este-Sur-Este-Sur)— Sudeste por el Este
SEpS/SEbS (Sur-Sur-Este-Este)— Sudeste por el Sur

(Sursureste)

SpE/SbE (Sur-Sur-Este-Sur)— Sur por el Este
SpO/SbW (Sur-Sur-Oeste-Sur)— Sur por el Oeste

(Sursuroeste)

SOpS/SWbS (Sur-Sur-Oeste-Oeste)— Sudoeste por el Sur
SOpO/SWbW (Oeste-Sur-Oeste-Sur)— Sudoeste por el Oeste

(Oestesuroeste)

OpS/WbS (Oeste-Sur-Oeste-Oeste)— Oeste por el Sur
OpN/WbN (Oeste-Norte-Oeste-Oeste)— Oeste por el Norte

(Oestenoroeste)

NOpO/NWbW (Oeste-Norte-Oeste-Norte)— Noroeste por el Oeste
NOpN/NWbN (Norte-Norte-Oeste-Oeste)— Noroeste por el Norte

(Nornoroeste)

NpO/NbW (Norte-Norte-Oeste-Norte)— Norte por el Oeste

El rumbo

Artículo principal: Rumbo

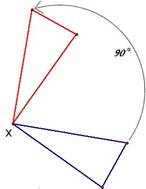
Un rumbo queda determinado por los puntos cardinales de la rosa de los vientos, cada uno de los cuales tiene establecido un valor numérico o ángulo en función de los siguientes criterios:
1. La dirección NORTE es el ángulo 0º o 360º.
2. En sentido horario, se forma un ángulo tomando de referencia N y que varía desde 0º hasta 360º.
3. En sentido horario, se forma un ángulo tomando de referencia N y que llega hasta S, varía desde 0º hasta 180º.

4. En sentido antihorario, se forma un ángulo tomando de referencia N y que llega hasta S, varía desde 0º hasta 180º.
5. En sentido horario, se divide la rosa de los vientos en 6400 partes, a este rumbo se le denomina indicación en mil angular o en milesimas de artillería partiendo de la referencia N como 0º. La división de la circunferencia en 6400 milésimas da lugar a que todos los puntos cardinales son un múltiplo exacto de esta unidad angular, ver la figura.

Sectores (en grados sexagesimales) correspondientes a cada viento

Viento del norte o Tramontana (N): de 337.5° a 22.5°
Viento del noreste o Gregal (NE): de 22.5° a 67.5°
Viento del este o Levante (E): de 67.5° a 112.5°
Viento del sureste o Siroco (SE): de 112.5° a 157.5°
Viento del sur u Ostro (S): de 157.5° a 202.5°
Viento del suroeste: Lebeche o Garbino (SW): de 202.5° a 247.5°
Viento del oeste o Poniente (W): de 247.5° a 292.5°
Viento del noroeste: Maestro o Mistral (NW): de 292.5° a 337.5°

Stellæ maris (Las estrellas del mar)

Punto cardinal	Estrella	Constelación
N	Polar	Alpha ursæ minoris
NpE/NbE	"Guardianas de la Osa" (Dubhe y Merak)	Alpha y Beta ursæ maioris
NNE	Dubhe	Alpha ursæ maioris
NEpN/NEbN	Schedar	Alpha cassiopeiæ
NE	Capella	Alpha aurigæ
NEpE/NEbE	Vega	Alpha lyrae
ENE	Arturo	Alpha bootis
EpN/EbN	Las Pléyades	Tauro
E	Altair	Alpha aquilae
EpS/EbS	Cinturón de Orión (Alnitak, Alnilam y Mintaka)	Delta, Epsilon y Zeta orionis
ESE	Sirio	Alpha Canis Majoris
SEpE/SEbE	Acrab	Beta scorpii
SE	Antares	Alpha scorpii
SEpS/SEbS	Rigil Kent(aurus)	Alpha centauri
SSE	Canopo	Alpha carinæ
SpE/SbE	Achenar	Alpha eridani
S	Cruz del Sur

Los navegantes árabes del Mar Rojo y Océano Índico dependieron más de la navegación celeste, en vez de los vientos, usaron la rosa de 32 puntos antes de finales del siglo décimo.
Las orientaciones estaban basadas en las posiciones de orto y ocaso de una serie de estrellas brillantes e incluso asterismos como las Pléyades, el Cinturón de Orión o la Cruz del Sur.
² ³ ⁴ ⁵ ⁶ En el hemisferio norte, la presencia de la estrella Polar (Polaris) fue usada para calcular el eje meridiano N-S; sin embargo, la cambiante posición de la Cruz del Sur es lo que se tiene para el hemisferio sur, como la estrella polar meridional está Sigma Octantis que es demasiado débil para ser vista fácilmente a simple vista. Los otros treinta puntos siderales se determinan por el orto y puesta de la posición de quince estrellas brillantes del hemisferio boreal. Leyendo de Norte a Sur, en sus posiciones tanto de orto como de ocaso, así queda en la tabla adjunta.⁷

Uso de la rosa de los vientos en el diseño de los aeropuertos

Se realiza un análisis de vientos con datos estadísticos de intensidad y dirección del viento en el lugar del emplazamiento, medidos durante un periodo de tiempo de al menos 5 años y como mínimo 8 veces diarias con intervalos iguales.Si no es posible realizar las mediciones en el propio emplazamiento, se podrán utilizar estadísticas de lugares cercanos donde haya un observatorio, teniendo en cuenta que puede haber diferencias entre las condiciones del entorno respectivas.
Estas observaciones se agrupan en intervalos de intensidad de velocidad, medida en nudos, y para las direcciones se divide cada cuadrante (N, S, W, E) en 4 sectores, de modo que se tienen 16 sectores de dirección de viento (nº de observaciones y frecuencias).
La representación gráfica de estos datos de intensidad y dirección de vientos se confecciona llevándolos a un diagrama de círculos concéntricos, cuyos radios son a escala las frecuencias de las observaciones en en cada sentido. Este diagrama es conocido como rosa de vientos.⁸

Anexo: Tabulación angular de los puntos cardinales por cuadrantes

La circunferencia de la rosa de los vientos se mide angularmente en sentido horario partiendo del cénit (12 horas) donde se coloca el punto N (norte).

El primer cuadrante es el cuadrante superior derecho de la circunferencia y conecta los puntos N y E (este)(3 horas).
El segundo cuadrante es el cuadrante inferior derecho de la circunferencia y conecta los puntos E y S (sur) o nadir (6 horas).
El tercer cuadrante es el cuadrante inferior izquierdo de la circunferencia y conecta los puntos S y W (oeste)(9 horas).
El cuarto cuadrante es el cuadrante superior derecho de la circunferencia y conecta los puntos W y N o cénit (12 horas).

Los sistemas de medición de ángulos aquí tabulados son los siguientes:
1. Sistema sexagesimal: Que otorga un valor de 360º (grados) a la circunferencia, 60" (segundos) son 1' (minuto) y 60' son 1º (grado).
2. Sistema centesimal: Que otorga un valor de 400^g (gonios) a la circunferencia, 100^cc (segundos centésimos) son 1^c (minuto centésimo) y 60^c son 1^g (gonio).
3. Sistema Mil artillero: Que otorga un valor de 6400‰ (por miles) a la circunferencia completa, 1‰ equivale a 2' 48.75" y a 6^c 25^cc, por eso no se usan submúltiplos.

PRIMER CUADRANTE N-E

Ángulo sexagesimal	Ángulo centesimal	Ángulo artillero	Abreviatura	Punto cardinal
0º	0^g	0‰	N	Norte
11º15'	12^g50^c	200‰	NpE	Norte por Este
22º30'	25^g	400‰	NNE	Nornoreste
33º45'	37^g50^c	600‰	NEpN	Noreste por Norte
45º	50^g	800‰	NE	Noreste
56º15'	62^g50^c	1000‰	NEpE	Noreste por Este
67º30'	75^g	1200‰	ENE	Estenoreste
78º45'	87^g50^c	1400‰	EpN	Este por Norte
90º	100^g	1600‰	E	Este

SEGUNDO CUADRANTE E-S

Ángulo sexagesimal	Ángulo centesimal	Ángulo artillero	Abreviatura	Punto cardinal
90º	100^g	1600‰	E	Este
101º15'	112^g50^c	1800‰	NpE	Este por Sur
112º30'	125^g	2000‰	ESE	Estesureste
123º45'	137^g50^c	2200‰	SEpE	Sureste por Este
135º	150^g	2400‰	SE	Sureste
146º15'	162^g50^c	2600‰	SEpS	Sureste por Sur
157º30'	175^g0^c	2800‰	SSE	Sursureste
168º45'	187^g50^c	3000‰	SpE	Sur por Este
180º	200^g	3200‰	S	Sur

TERCER CUADRANTE S-W

Ángulo sexagesimal	Ángulo centesimal	Ángulo artillero	Abrev.internacional	Punto cardinal
180º	200^g	3200‰	S	Sur
191º15'	212^g50^c	3400‰	SbW	Sur por Oeste
202º30'	225^g	3600‰	SSW	Sursuroeste
213º45'	237^g50^c	3800‰	SWbS	Suroeste por Sur
225º	250^g	4000‰	SW	Suroeste
236º15'	262^g50^c	4200‰	SWbO	Suroeste por Oeste
247º30'	275^g0^c	4400‰	WSW	Oestesuroeste
258º45'	287^g50^c	4600‰	WbS	Oeste por Sur
270º	300^g	4800‰	W	Oeste

CUARTO CUADRANTE W-N

Ángulo sexagesimal	Ángulo centesimal	Ángulo artillero	Abrev.internacional	Punto cardinal
270º	300^g	4800‰	W	Oeste
281º15'	312^g50^c	5000‰	WbN	Oeste por Norte
292º30'	325^g	5200‰	WNW	Oestenoroeste
303º45'	337^g50^c	5400‰	NWbW	Noroeste por Oeste
315º	350^g	5600‰	NW	Noroeste
326º15'	362^g50^c	5800‰	NWbN	Noroeste por Norte
337º30'	375^g0^c	6000‰	NNW	Nornoroeste
348º45'	387^g50^c	6200‰	NbW	Norte por Oeste
360º	400^g	6400‰	N	Norte

Galería

Rosa de los vientos de una vieja carta de navegación, por el cartógrafo portugués Pedro Reinel (1504)
Una rosa de los vientos histórica
Una rosa de los vientos de 8 puntos
Rosa de los vientos de 16 puntos con el norte señalado en la parte superior
Rosa de los vientos de 32 puntos
La rosa de los vientos más grande del mundo, dibujada en el suelo del desierto en la Base de la Fuerza Aérea Edwards en EE. UU.
Rosa de los vientos de 16 puntos
Rosa de los vientos internacional de 4 puntos
Rosa de los vientos internacional de 8 puntos
Rosa de los vientos internacional de 16 puntos
Rosa de los vientos internacional de 16 puntos
Rosa de los vientos internacional de 32 puntos
Rosa de los vientos de Seamus Macgill
Rosa de los vientos catalana
Rosa de los vientos con graduación

ento en diferentes sectores en los que divide el círculo del horizonte.

homotecia

Homotecia

Homotecia con centro O y λ>1.

Una homotecia es una transformación afín que, a partir de un punto fijo, multiplica todas las distancias por un mismo factor. En general una homotecia de razón (λ) diferente de 1 deja un único punto fijo, llamado centro.

Definición

Esquema de operación de una homotecia, en el plano euclídeo.

Sea E un espacio vectorial sobre un cuerpo

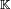\scriptstyle \mathbb{K}

. Sea X un elemento (visto como un punto) de E. La homotecía de centro C y de razón k, denotada

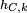\scriptstyle h_{C, k}

envía un punto M del espacio vectorial sobre el punto M' tal que: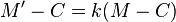

(1a) $M'- C = k(M-C)\,$

La ecuación anterior puede escribirse también como una transformación afín de la forma:

(1b) $M' = kM + (1-k)C \,$

La anterior relación puede escribirse vectorialmente en el plano como:

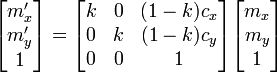
$\begin{bmatrix} m'_x \\ m'_y\\ 1 \end{bmatrix} = \begin{bmatrix} k & 0 & (1-k)c_x \\ 0 & k & (1-k)c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} m_x \\ m_y\\ 1 \end{bmatrix}$

Donde:

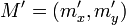M' = (m'_x, m'_y)\,

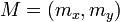M = (m_x, m_y)\,

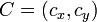C = (c_x, c_y)\,

.
En tres o más dimensiones la fórmula anterior se generaliza trivialmente.
Cuando el cuerpo de escalares son los Reales, una homotecia de centro el punto C y razón el número real k ≠ 0, es una transformación geométrica que hace corresponder a cada punto P otro punto P′ tal que (el vector es igual al resultado de multiplicar el vector por el número k). Si k es positivo, P′ está en la semirrecta de origen C que pasa por P.

Propiedades

La homotecia es una transformación afín, composición de una transformación lineal y una traslación, y por consiguiente conserva:

el alineamiento: las imágenes de puntos alineados son alineados: (A,B,C) y (A', B', C') en la figura
el centro de un segmento, y más generalmente el baricentro: la imagen del baricentro es el baricentro de las imágenes. En la figura, B es el centro de [A;C] y por lo tanto B' es el de [A';C']
La imagen de línea es otra línea paralela a la original.
el paralelismo: dos líneas paralelas tienen imágenes paralelas. En la figura (B'E') // (C'D') porque (BE) //(CD).
Si k ≠ 1, el centro de la homotecia es el único punto fijo (k = 1 corresponde a la identidad de E: todos los puntos son fijos).
k = - 1 corresponde a una simetría de centro C.
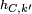Si k ≠ 0, $\scriptstyle h_{C, k}$ admite como trasformación reciproca $\scriptstyle h_{C, 1/k}$ (cuando k = 0, no es biyectiva).
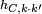Al componer dos homotecias del mismo centro se obtiene otra homotecia con este centro, cuya razón es el producto de las razones de las homotecias iniciales: $\scriptstyle h_{C, k}$ o $\scriptstyle h_{C, k'}$ = $\scriptstyle h_{C, k\cdot k'}$ .
Al componer homotecias de centros distintos, de razones k y k', se obtiene una homotecia de razón k·k' cuando k·k'≠1, y una traslación si k·k'=1. El conjunto de las homotecias (con k≠0) y las translaciones forman un grupo.

Cuando el cuerpo de escalares son los Reales, se cumple que:

todas las longitudes son multiplicadas por |k|, el valor absoluto de la razón.
el cociente de longitudes es conservado: A'C'/B'E' = AC/BE en la figura
los ángulos orientados son conservados, en particular los ángulos rectos. Es obvio en la figura.

Más aún:

k = - 1 corresponde a la simetría de centro C que es la rotación alrededor de C de ángulo π radianes (180º).
|k| > 1 implica una ampliación de la figura.
|k| < 1 implica una reducción.
k < 0, la homotecia se puede expresar como la composición de una simetría con una homotecia de razón |k|, ambas de igual centro. Que la homotecia original.

Homotecias en el plano real

En esta sección, los escalares serán números reales.
Una homotecia generalizada en el plano es una transformación del plano en sí mismo en donde una recta y su homóloga son paralelas. De esta definición, se sigue fácilmente que las homotecias conservan ángulos, es decir son transformaciones conformes del plano, que el conjunto de homotecias forman un 'grupo' y que las traslaciones son casos particulares de las homotecias.
Consideremos la homotecia en la cual la recta OA se transforma en la recta O'B, siendo O' el homólogo de O y B el homólogo de A. Necesariamente, las rectas OO' y AB son invariantes en esta homotecia y el punto H1, centro de la homotecia, es invariante. En esta homotecia la circunferencia de centro O y radio OA se transforma en la circunferencia de centro O' y de radio O'B y la razón de la homotecia es la razón (positiva) de los segmentos O'B y OA.
Si por el contrario, el punto A se transforma en B' entonces la recta AB' es invariante y es el punto H2 el centro de homotecia. En este caso, la razón de la homotecia es negativa.

Ejes de homotecia

Dadas dos circunferencias, éstas siempre se pueden considerar como homotéticas una de la otra.
En la figura, la circunferencia S2 puede considerarse homotética de s1 bien es en la homotecia de razón positiva, con centro en P1, o de razón negativa, con centro de homotecia en N1.
Consideremos las homotecias, una con centro en P1 en la cual la circunferencia S2 es homotética de la circunferencia s1, y la homotecia de centro P3 en la que la circunferencia s3 es homotética a la circunferencia s2. La composición de estas dos homotecias es la homotecia de centro en P2 que transforma la circunferencia s1 en la circunferencia s3. Es por esta razón que los centros de homotecia positivos, P1, P2 y P3 están alineados. En general, dadas tres circunferencias existen seis centros de homotecia, alineados tres a tres sobre cuatro rectas.
Estas rectas son las llamadas ejes de homotecia de las tres circunferencias dadas

rotacion

Rotación del triángulo, respecto del punto X.

Transformaciones isométricas por Rotación

Una rotación, en geometría, es un movimiento de cambio en la orientación de un cuerpo; de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo, y tiene las siguientes características:
Un punto denominado centro de rotación.
Un ángulo
Un sentido de rotación.
Estas transformaciones por rotación pueden ser positivas o negativas dependiendo del sentido de giro.
Para el primer caso debe ser un giro en sentido contrario a las manecillas del reloj, y será negativo el giro cuando sea en sentid

Dados un punto O y un ángulo α, se llama giro de centro O y ángulo α a una transformación G que hace corresponder a cada punto P otro P' = G(P) de modo que:
expresiones

El sentido de giro positivo de es del contrario al movimiento de las agujas del reloj.
Los giros son movimientos isométricos, dado que conservan las distancias.

1 Giro de centro O(0,0)

2 Giro de centro O'(a,b)

Composición de giros

1 Con el mismo centro

Al aplicar sucesivamente dos giros de igual centro O y amplitudes α y β se obtiene un giro de igual centro O y amplitud igual a la suma de las amplitudes α+β .

2 Con distinto centro

o de las manecillas.

atp2014-13

miércoles, 15 de octubre de 2014