rotacion

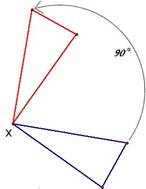
Rotación del triángulo, respecto del punto X.

Transformaciones isométricas por Rotación

Una rotación, en geometría, es un movimiento de cambio en la orientación de un cuerpo; de forma que, dado un punto cualquiera del mismo, este permanece a una distancia constante de un punto fijo, y tiene las siguientes características:
Un punto denominado centro de rotación.
Un ángulo
Un sentido de rotación.
Estas transformaciones por rotación pueden ser positivas o negativas dependiendo del sentido de giro.
Para el primer caso debe ser un giro en sentido contrario a las manecillas del reloj, y será negativo el giro cuando sea en sentid

Dados un punto O y un ángulo α, se llama giro de centro O y ángulo α a una transformación G que hace corresponder a cada punto P otro P' = G(P) de modo que:

El sentido de giro positivo de es del contrario al movimiento de las agujas del reloj.
Los giros son movimientos isométricos, dado que conservan las distancias.

1 Giro de centro O(0,0)

2 Giro de centro O'(a,b)

Composición de giros

1 Con el mismo centro

Al aplicar sucesivamente dos giros de igual centro O y amplitudes α y β se obtiene un giro de igual centro O y amplitud igual a la suma de las amplitudes α+β .

2 Con distinto centro

o de las manecillas.